The ancient megaliths of Brittany have long fascinated researchers and enthusiasts alike. Among those who have delved deeply into their mysteries is Quentin Leplat, whose documentary Arpenteurs du Néolithique (Surveyors of the Neolithic), available on YouTube (in French), offers an insightful exploration into these enigmatic structures. Quentin Leplat's work, also published in an article on Academia, and supplemented by follow-up videos (see here for the first), presents compelling evidence that these megalithic sites were not isolated monuments but part of a vast, interconnected network shaped by advanced knowledge of geometry and astronomy. His investigations reveal a sophisticated understanding of space and alignment, prompting a reevaluation of how prehistoric people perceived and interacted with their environment.

One of the most intriguing aspects of this research is the geometric precision underlying these ancient constructions. Researchers like Howard Crowhurst have contributed significantly to this field, demonstrating how megalithic builders employed complex mathematical principles, particularly the use of squares, double squares, and triple squares, and so on, to form rectangles which were the basis of the ground geometry. This geometric approach suggests that the positioning of dolmens, menhirs, and other structures was not arbitrary but followed a deliberate spatial logic, connected to geometry and astronomical cycles.

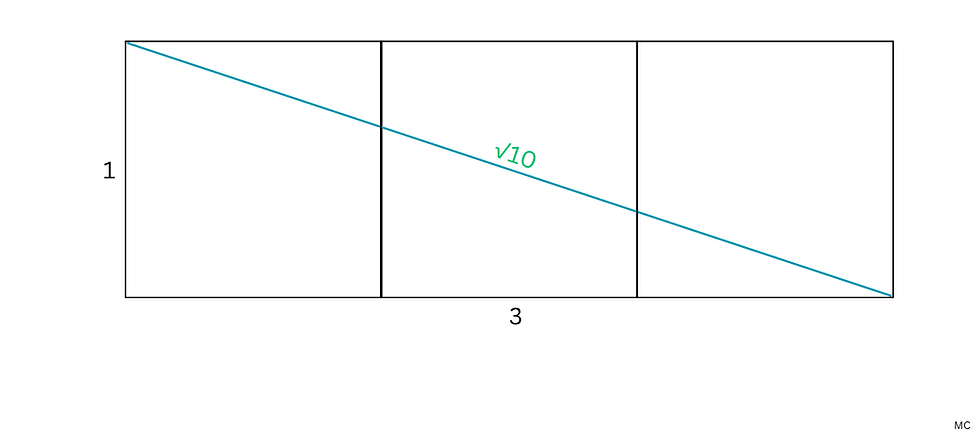
During his study of the dolmens in the commune of Plouharnel, Morbihan, Quentin Leplat identified an alignment of four dolmens spanning 7 817 metres. While the region contains many recorded dolmens, statistical chance alone does not account for the extraordinary precision of this alignment. Measured with both Google Earth and high-precision GPS, the dolmens follow a straight line with an angular deviation of only ±0.07°, corresponding to a narrow corridor just 4 metres wide.

Beyond the sheer accuracy of placement, the spacing of the dolmens suggests an underlying geometric principle. The distances between them follow a proportional sequence based on the square root of 10 (√10). This relationship, along with connections to ancient measurement units and celestial cycles, indicates an advanced understanding of mathematics, geometry, and astronomy among the Neolithic builders. This article seeks to present Quentin Leplat's work on this alignment, look at the geometry and dimensions, and reflect on what the intention of the surveyors may have been.

The Geometry of the Alignment

Understanding this region's megaliths requires moving beyond an isolated-site perspective and instead recognising them as nodes in a vast spatial and cultural network. The dolmens and other structures appear to be precisely placed within the terrain. Their distribution suggests that Neolithic builders possessed a deep understanding of astronomy, allowing them to track important solar and lunar cycles. Many of these sites align with solstices, equinoxes, and significant lunar standstills, reinforcing the idea that their placement was far from coincidental. By analysing these structures through the lens of geometry and astronomy, we can begin to decipher their purpose. The dolmens and standing stones of Brittany were likely not just burial sites or territorial markers but part of a much grander system of knowledge transmission, functioning as reference points in a landscape designed to encode celestial movements, as part of an ancient observatory system that connected terrestrial and cosmic rhythms.

This reinterpretation of the Breton megaliths challenges conventional archaeological assumptions and opens the door to a deeper understanding of prehistoric science, spirituality, and society. By studying these sites as an integrated whole, rather than in isolation, we can gain valuable insights into the intellectual and cultural achievements of the Neolithic world.

The Structure of the Line

The alignment consists of four dolmens:

• Kergazec

• Mané er Mor

• Runesto

• Mané-Roularde

  
  

Quentin Leplat focused his analysis on these four dolmens because of their respective distances along the alignment. The first segment of the alignment, from Kergazec to Mané er Mor, is precisely 1/10th of the total length (718.7 metres out of 7 817 metres). The second segment, from Kergazec to Runesto, is 2 472 metres, demonstrating the presence of the factor √10 (square root of ten).

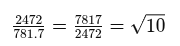
This mathematical relationship is not arbitrary. The diagonal of a triple square (a rectangle composed of three squares side by side) is precisely √10 times the side length of one square. This suggests that the builders were using a sophisticated modular design based on geometric principles. Additionally, when analysing the azimuth of the alignment, Quentin Leplat applied his expertise in ancient geometry and found that its angle (21.825°) closely corresponds to the diagonal of a 2 x 5 rectangle of squares (21.801°), reinforcing the theory of a deliberate use of a structured geometric plan. These ratios are precise, and prove that the builders of these dolmens had a sophisticated knowledge of geometry.

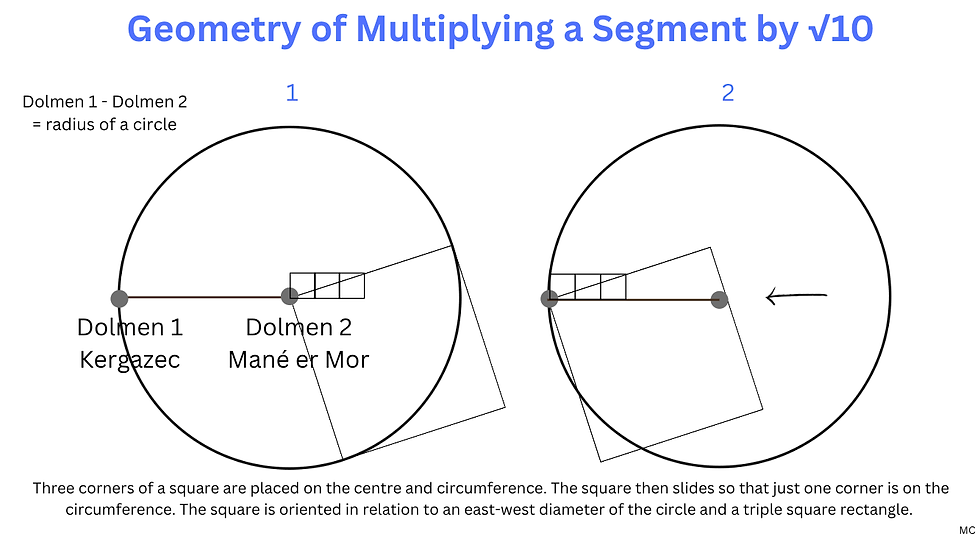
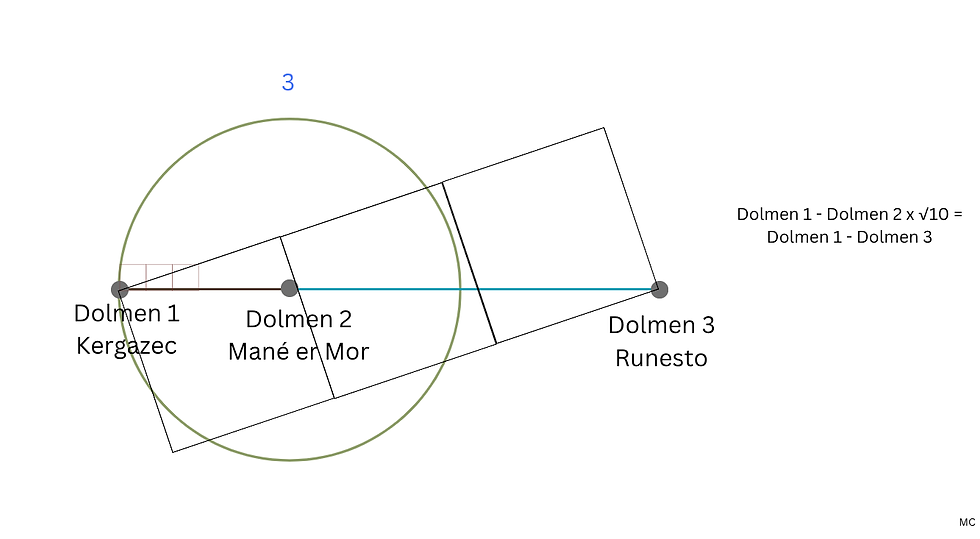
I wanted to visualise the connection between multiplying a segment by the square root of ten and the square root of ten being, geometrically, the diagonal of a 1 x 5 rectangle. So I experimented with a few constructions, and found that the first segment of the ailignment, between the first two dolmens, can be taken as the diameter of a circle. Then, a square is inscribed, so that three of its corners touch the centre and circumference of the circle. The square is oriented in relation to a triple square, to get the right angle, and shifted so that only one corner touches the circumference. The square is then extended into a 3 x 1 rectangle (three squares side by side), and the diagonal drawn. This diagonal then corresponds to the second segment of the alignment, between dolmens 2 and 3. Then the same process is repeated to get the third segment, and the position of dolmen 4.

Landscape Considerations: Visibility and Elevation

   When I watched Quentin Leplat's film, I thought that one of the most striking features of this alignment was that all four dolmens are placed at high points in the landscape along the line. This positioning ensures their visibility from great distances, reinforcing the idea that these were deliberate markers rather than randomly placed structures. This strategic placement suggests an advanced survey method. These dolmens were therefore most likely visual markers.

What can the dimensions tell us?

Connections to Ancient Measurement Systems

The measured distances align closely with the megalithic yard (MY), identified by Professor Alexander Thom in megalithic sites across Europe. The alignment corresponds to the diagonal of a rectangle composed of two squares by five squares, where each square has a side measuring 1 451.6 metres. This can be interpreted as 7 000 / 4 megalithic yards. Furthermore, the alignment's total length of 7 817 metres establishes a connection between the megalithic yard and the number π. This distance corresponds to the circumference of a circle with a diameter of 3 000 megalithic yards, as Quentin Leplat has shown.

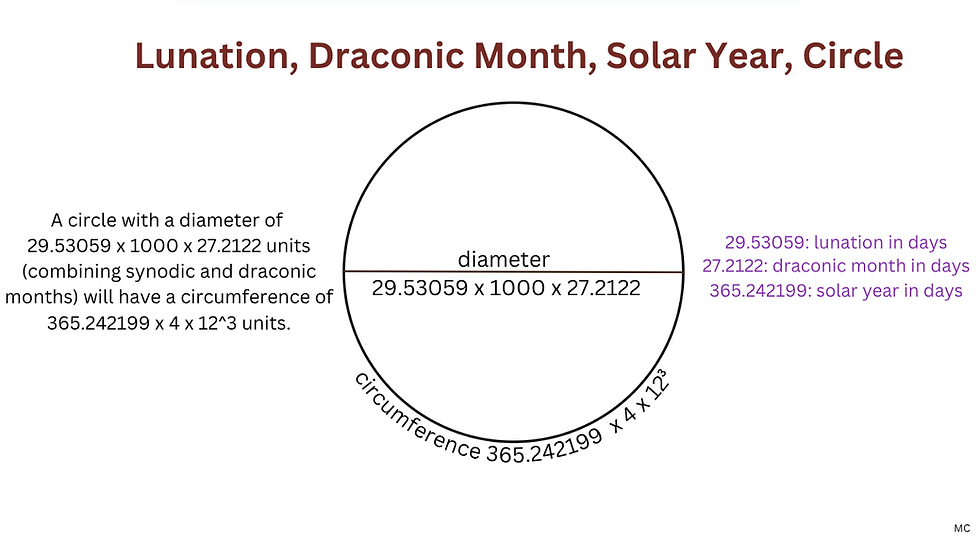
 The draconic month expressed in days, multiplied by 6/5, and interpreted as a value in inches, gives 32.65464, a value acceptable as a megalithic yard. And as Quentin Leplat has observed, the first segment corresponds to the circumference of a circle with a diameter of 300 MY. Another way of looking at this is to take a line of 365.242199 x 4 x 12^3 / (29.53059 x 1000) inches and divide it by 2.61803, Phi squared. This gives a result of 32.654116 inches, which is a megalithic yard in inches. (2.721176 feet). This works because of the 5/6 approximate connection between pi and Phi squared.

Inches, metres and other units can also be considered to interpret the dimensions of this line. A compelling mathematical relationship emerges from a comparison of three astronomical cycles, the draconic month (27.2122 days), the lunation or synodic month (29.53059) and the tropical solar year (365.242199 days): The mean number of lunations per year (365.242199 / 29.53059) is very close to the draconic month expressed in days multiplied by 1000 π / (12³ x 4).

27.2122 x 1000 π / (12³ x 4) ≈ 365.242199 / 29.53059

This is not perfectly exact, as 27.2122 x 1000 π / (12³ x 4) x 29.53059 = 365.24302, but it is very close, a 99.999775% match.

If we think of these values as measures in inches, and look at various parts of this equation, we can very closely approximate other important units of measure.

• 27.2122 x 10 000 / (12³ x 4) = 39.369502, very close to a metre. (1 metre is 39.3700787402 inches)

• 365.242199 / (29.53059 π) x 10 = 39.369414, very close to a metre

• And we can link this to another astronomic and geometric equation, involving the sidereal month of 27.321661 days as well as a lunation, and 235, the number of lunations in a Metonic cycle: 10 000 / (235 x 29.53059 / 27.32166) = 39.370154. This is also very close to a metre in inches.

• It's also possible to interpret the megalithic yard and the French foot (pied de roi) in relation to a draconic month.

  
  

So we could interpret the first segment of alignment also as:

• 12⁵ π / 1000 = 781.7287 metres (perhaps a bit on the large side, and so can perhaps be discounted as a possible interpretation)

  
  

• 12⁵ / 100 x 365.242199 / 29.53059 = 30 776.2042 inches (781.7156 m)

  
  

• 360 π x 27.2122 = 30 776.2731 inches (781.7174 m)

  
  

These last two options offer two ways to interpret the dimensions of the alignment in relation to astronomy and the inch, to a high degree of precision, with one inch representing a day. Elsewhere, particularly in Brittany and Egypt, the inch has been identified as a unit corresponding to one day (1). When read as measures in inches, the metre and megalithic yard can be understood as astronomical measures. A metre for example can be approximately seen as the average number of lunations per year, multiplied by 10 and divided by π, as a measure in inches. A megalithic yard can be understood as the average number of lunations per year divided by π also, but then multiplied by 12⁴ x 4 / 10 000. The megalithic yard can also be understood as a draconic month in days multiplied by 6 / 5, again as a measure in inches. As a result of these connections, it is interesting to note that the first segment of he alignment, and the total length, which is ten times the first segment, can be understood in relation to the average number of lunations per year (365.242199 / 29.53059), or the draconic month in days and π. The interpretations of these units of measure seem to respond to the same logic as the interpretation of the lengths in the alignment.

Quentin Leplat's study explores the geometric relationships present in megalithic structures, demonstrating that their layouts reflect sophisticated knowledge of metrology and astronomical cycles. Specifically, the megalithic yard may have been derived from lunar and solar periodicities, linking architectural design to celestial observations. By summarising these core insights upfront, readers can better contextualise the subsequent technical discussions and appreciate the broader implications of this research.

Metrological Considerations: The Inch as a Time Unit

What could be the purpose of this alignment, almost eight kilometres long? One compelling possibility is that the alignment encodes lunar nodal cycles. The Moon's orbit crosses the ecliptic at two points (nodes), which regress over an 18.6-year cycle. The draconic month, which measures the time between two successive crossings of the same node, is 27.2122 days. We've seen that this cycle can be linked to a linear measure: 360 x 27.2122 π = 30 776.27, and as a measure in inches, this is exactly 781.7173 metres, which is the length between the first two dolmens (781.7 m), and a tenth of the whole alignment. The first segment multiplied by √10, is 2 472.007 metres, the distance between the first and third dolmen (2 472 m), and multiplied by 10, this is the total distance (7 817 m).

1. A synodic month interpretation

The length of the alignment, 7817 metres, the first segment is a tenth of the whole, and can also be interpreted as 12⁵ / 100 x 365.242199 / 29.53059 = 30 776.2042 inches, with an inch representing a day. This is the average number of lunar months in a year (365.242199 / 29.53059) expressed in inches, multiplied by 12 to the power of 5, and divided by 100. The imperial system is also partly duodecimal, so there is an interesting connection there.

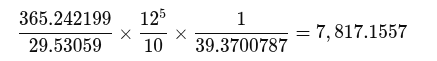
2. A draconic month interpretation

   
   

  If the first segment can be interpreted as 360 π x 27.2122 = 30 776.2731 inches, the 360 represents the degrees in a full circle, π relates to circular motion, and 27.2122 to the draconic month in days. (30 776.273 inches are 781.71734 metres)

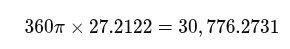
A compelling possibility is that the alignment encodes lunar nodal cycles, which were crucial for predicting eclipses. The Moon’s orbit is tilted relative to the Earth's orbit around the Sun, and its path crosses the ecliptic at two points, known as nodes. These nodes regress over an 18.6-year cycle, meaning that over this period, the nodes complete a full circuit backward along the ecliptic. Understanding this cycle is important for predicting eclipses, which only occur when the Sun is near a lunar node during a full or new moon.

A draconic month is the time between two successive crossings of the Moon through the same node, precisely 27.2122 days. The builders of these monuments may have used specific linear measures to encode astronomical knowledge.

The presence of 360 × π × 27.2122 in the first segment (and multiplied by 10 in the full alignment) suggests we could be dealing with something circular, periodic, and linked to the Moon’s motion, raising the question: what cycles or measurements could this equation represent? There are several possibilities for how this relates to lunar cycles and astronomical observation. Each of the following cycles plays a role in lunar movement, and we will examine how they might connect to the equation:

1. Lunar Node Precession (18.6-Year Cycle). The lunar nodes (the points where the Moon’s orbit crosses the ecliptic) gradually move backward through the zodiac over 18.6 years due to gravitational interactions. This cycle determines when and where eclipses can occur over long timescales. A physical representation of this might involve marking draconic months at regular intervals along a line, showing how the nodes shift over time.

2. The Moon’s Distance from Earth. The Moon’s orbit is elliptical, meaning its distance from Earth changes cyclically. This variation follows the anomalistic month (~27.55 days), close to the draconic month. Could the alignment represent variations in lunar distance over time? This would be another way to connect angular motion (360°) with a periodic oscillation.

3. Connection to the Sidereal Month (27.3217 Days). The sidereal month is the time it takes the Moon to return to the same position relative to the stars. The ratio between the draconic month (27.2122 days) and the sidereal month (27.3217 days) accumulates over time, influencing eclipse cycles. A physical alignment could track these gradual shifts by marking intervals of draconic months while showing how they diverge from sidereal cycles.

4. Angular Motion and 360° as a Unit of Time-Space Conversion. The Moon completes 360° in its orbit roughly every 27.3 days (sidereal month). If we take one draconic month (27.2122 days) and multiply it by 360, we get an angular measurement in time: 360 × 27.2122 = 9796.4360. This number could be converted into a linear distance, representing how far the Moon moves in its orbit over that period. This suggests a system where time is converted into spatial units, possibly with π acting as a conversion factor.

5. Ratios to Other Cycles (Metonic & Saros Cycles). The Metonic Cycle (19 years, ~235 lunar months) aligns the solar and lunar calendars. The Saros Cycle (18 years, 11 days, ~223 lunar months) is the repeating cycle of eclipses. The draconic month plays a role in both cycles, particularly the Saros cycle, where eclipses reoccur at almost the same location in the sky after 18 years, 11 days. The equation might encode a way to track these periodic eclipse returns by marking draconic months in a linear or geometric pattern.

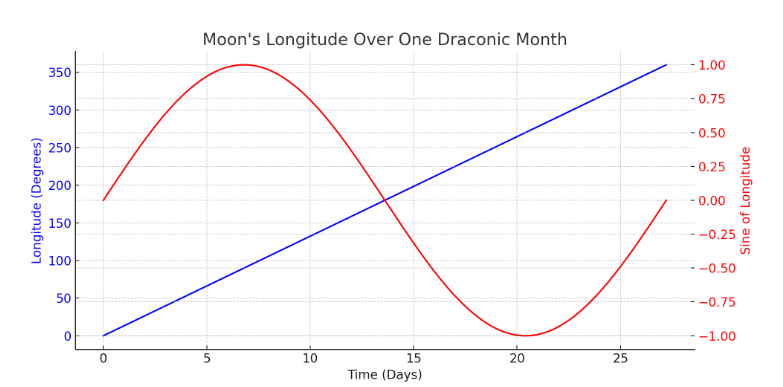
6. Latitude and longitude of the moon. The elliptical orbit causes speed variations in longitude (~12°-15° per day). Picking up on these variations observed in the sky, observers would have deduced the orbit was elliptical. Understanding this motion is crucial for eclipse prediction, as the Moon’s return to a node determines when an eclipse might occur.

The graph above shows the Eastward Motion (Blue Curve): The Moon moves roughly 13.2° per day, completing 360° in longitude over about 27.21 days. Also, it shows the Nodal Crossings (Red & Purple Dashed Lines):

• Ascending Node (0 days) → The Moon crosses the ecliptic moving northward.

• Descending Node (~13.6 days) → The Moon crosses southward.

• The graph also shows the elliptical speed variation, with the perigee (Green Point, ~Day 5) → The Moon moves faster (~14°/day), and apogee (Orange Point, ~Day 19) → The Moon moves slower (~12°/day).

This shows how the Moon’s longitudinal motion isn’t uniform due to its elliptical orbit, but it still averages 360° per draconic month. If this movement were precisely studied it would have become clear that the moon moves in an ellipsis, not a circle.

Below is a graph of lunar longitude versus time over one draconic month (27.2122 days). The motion is mostly linear, representing the Moon's mean motion of about 13.23° per day, but with a small sinusoidal variation due to its elliptical orbit. The graph below also shows the moon's longitude over a draconic month, but with a second type of line, showing the sine of longitude, which brings pi into the equation.

What I imagined was that the alignment was like a giant x-axis on a graph, measuring the draconic month in days, and tracking longitude over time, allowing observers to track the moon's position daily, and visualise its motion, as it returns to the same node after 27.2122 days. Perhaps some observations were made on the one month segment of the line, between the first and second dolmens, and others over a ten draconic month period, the entire line. The moon completes a full 360° revolution in longitude roughly every sidereal month (27.3 days), so it’s a useful reference for tracking full cycles, but in a draconic month, the moon returns to the same node after about 27.2122 days, meaning the longitude cycles around a full 360° relative to the lunar nodes. The moon's oscillations in latitude follow a sinusoidal pattern, meaning that π is inherent in how its motion is described mathematically. The fundamental shape of a sine wave is directly linked to the ratio of a circle’s circumference to its diameter, π. If the Moon’s orbit was being tracked using this method, π could be a hidden component in converting linear motion to cyclical patterns. While longitude follows a more linear progression, it can still be useful to describe periodic cycles, such as half a cycle being about 180° (or π radians). It puzzled me that both π and the number 360 should be included in the measurement, presumable the 360 being about the degrees of a circle. Perhaps we are dealing with two different but related ways of measuring circular motion: a 360° system, in degrees, reflecting the 360° journey in longitude approximately every sidereal or draconic month, and also a π-based system, using radians, a system which works well with wave motion, oscillations, and sinusoidal behaviour (such as the Moon’s oscillation in latitude). So on the one hand, an observer could measure where the moon was in its orbit, using the 360° system for a complete rotation, and on the other hand the wave-like pattern of the moon's motion could be tracked and expressed in π-based terms (since a full sine wave is 2π radians). If the daily motion of the Moon in longitude (about 360° / 27.2122 ≈ 13.23° per day) is equivalent to 0.231π radians per day, its motion over time can be described using either system. if we graph the Moon’s longitude over time, it oscillates up and down in latitude in a sinusoidal pattern. This is naturally expressed using π. Perhaps 360 markers would have been placed along the line (assuming the ground could somehow be made flat, perhaps with rope or wood), so as to map the degrees of rotation in a cycle in relation to, say, longitude, or some other aspect of the moon's movement in a draconic month, and then a sinusoidal function where longitude varies with time could also somehow be marked out, to understand periodic motions and predict eclipses. In short, if both π and 360° both show up in the interpretation in inches of the alignment's dimensions, alongside the draconic month in days, perhaps the purpose of the alignment was to track lunar cycles, and describe the motion of the moon within the cycle, in a sort of 3D, human-sized graph.

The Role of the Square Root of 10 in Megalithic Timekeeping?

A key mathematical feature emerging from this study is the role of the square root of 10 as a proportional factor linking sections of the alignment. The first segment of the system, perhaps rooted in the draconic month, eclipse cycles, and the 360-degree framework, would represent a lunar-based timekeeping structure. By multiplying by √10​, this lunar framework transitions into a solar-year-based system (365 days) with an additional connection to Venus’s 8-year cycle and an 800-year periodicity. This proportional relationship suggests that the megalithic builders may have encoded a geometric scaling principle that allowed for the conversion of lunar measurements into solar and planetary cycles. Such a system would provide a sophisticated means of tracking long-term celestial rhythms, potentially integrating lunar eclipses, Venusian phases, and solar periodicities into a unified astronomical model expressed through site geometry.

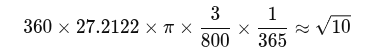
Here are two key equations that illustrate how the square root of 10 may possibly act as a proportional factor linking lunar, solar, and Venusian cycles. Starting with a lunar-based framework, we can consider the product of the draconic month of 27.2122 days, the 360° angular system, and π:

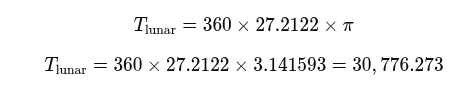
Multiplying by √10​, we can then transition into a solar-related framework:

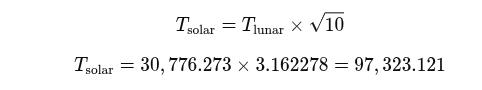
This number, 97 323.121, is close to 800 / 3 x 365, and corresponds to the distance between dolmens 1 and 3 in inches. The 8 year cycle, or octaeteris, related to the cycle of Venus, was a key component of ancient calendars. 800 years divided into three parts gives: 800 / 3 = 266.667.

The nodal period (full cycle of the lunar nodes returning to the same position) is 6798.38 days.

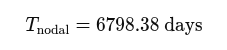
If this is divided by 17, the result is 399.905. close to 400. A draconic month, 27.2122 days, multiplied by 49 is very close to 4 000 / 3, and so 49 x 3 draconic years are almost exactly 4 000 days. This confirms that the nodal period (6,798.38 days) can be structured around multiples of the draconic month (27.2122 days) and the numbers 17, 49, 4 and 3. This suggests that the nodal period may have been incorporated into megalithic timekeeping through harmonic scaling, a compelling mathematical structure tying together lunar cycles and long-term eclipse periodicity.

These equations support the idea that the megalithic builders used geometric scaling and harmonic relationships to unify different celestial cycles

Conclusion: A Monument to Mathematics and Astronomy

The alignment of Plouharnel is not merely a remarkable example of Neolithic surveying; it is a testament to advanced knowledge of geometry, metrology, and celestial cycles. The presence of √10 suggests an intentional geometric principle, while the total alignment length ties directly to lunar cycles and ancient units of measurement.

Quentin Leplat's research highlights how these megaliths were part of a much larger pattern, not only within the landscape but within a sophisticated framework of measurement and astronomical observation. Whether used as a sightline for observation, a metrological system, or a way to track celestial cycles, this alignment demonstrates a level of mathematical sophistication that far exceeds what is commonly assumed about Neolithic cultures.

Future research should explore additional alignments in Brittany and beyond, testing whether similar patterns exist elsewhere. If so, it could redefine our understanding of megalithic science and its deep connections to ancient knowledge systems.

   The evidence presented in this study strongly suggests that the dolmens of Plouharnel were not randomly placed but were part of a deliberate, mathematically structured alignment. The integration of the square root of ten, ancient measurement systems, and astronomical cycles, particularly the draconic month, indicates an advanced understanding of geometry and celestial movements. These findings challenge conventional views of Neolithic societies, highlighting their potential sophistication in surveying, timekeeping, and space organisation. Further interdisciplinary research, incorporating archaeology, astronomy, and metrology, could shed even more light on the knowledge systems of prehistoric civilisations and their enduring impact on human history.

If you haven't watched Quentin Leplat's film Arpenteurs du Néolithique, please do. For non-French speakers, subtitles are available in the settings.

-

Notes

1. See Heath, Richard & Heath, Robin, 2010, "The Origins of Megalithic Astronomy as found at Le Manio " https://www.academia.edu/5384545/The_Origins_of_Megalithic_Astronomy_as_found_at_Le_Manio). Also, see https://www.mercurialpathways.com/post/84-the-inch-prehistoric-measure-of-time